Disclaimer: This is my interpretation of the concepts in computer and networking the way I understand it. Everyone has a different understanding of the topics, and how everyone sees something could be different; I am just showing this from my perspective. Of course, what I understood could very well be misinformed or totally wrong. Please do not treat what you see here as fact and always do your own research. These should be for entertainment and comedic purposes only 😉. Enjoy!

Welcome back, everyone🥳 to Noob 101 series. As always, I’m your host for today, Professor Laz.
Today, we will be talking about Binary operations as I promised in the previous lesson. Truth be told, I thought I would have this out sooner, but I guess I took a nap for a bit longer than I expected and did not wake up until now 😅. Oh well! Better late than never, am I right?
Here is today lesson’s agenda:
- What is Binary Operations?
- How does computer do the Operation?
- Additon
- Subtraction
- Converting binary into base 10 number
What is Binary Operations?
You see, in a computer’s language (not a coding langue), binary is just a number that represents a value. Just like how we use numbers and letters to express our understand and create so many amazing things by putting letters together. Computer language is doing the same thing but with only limited options of 0 and 1. I know it sucks to only be able to express anything with just two choices, but that is due to the limitation of how computers understand and receive inputs which I mentioned back in the first lesson Here. So how do we get around that limitation and create more rich expressions? By putting more of it together, of course, 😂. We combine letters and make words, so computers combine 0 and 1 to make words and numbers. For example, 00 is 0, and 01 is 1, but 10 is 2, and 11 is 3, or they can understand our alphabet letter with a string (just a bunch of them together) of binary such as “A” = “01000001”. Fascinating, isn’t it? You know what they say if you can’t do something with just 0 and 1, then just get more of it 😉.
We called computers “Computer” for a reason. Why? Because we are using them to compute or do math and calculation. I know, right? It literally means what is, but many people overthink many things. But it does get complex when we put simple things together too, so we have to know that.
Computers use binary as their primary language (no secondary language yet), so I’m sure most of us did learn how to do the basic math back in kindergarten (or older than that 🤷♂️) of addition and subtraction. Addition and subtraction, multiplication, division… are what we call operations, and well, it is the same for Binary operation. Instead of 2+2, we have 10 + 10 (this is 2 + 2 in binary, by the way). So Binary operation is just the same as our math operation (add, subtract, multiply, divide), but instead of regular numbers, it uses binary because it can only do binary 🤣.
How does computer do operations?
If you have read my previous lesson about binary, you would have made the connection between how the computer takes the inputs (0 or 1) and transforms them into the desired output (0 or 1) using logic gates. So what can we do with that? It is potent since we can put them together and make many beautiful things as long as we understand the fundamentals. Here is an example of the implementation of logic gates to do addition operations I found from the 101computing.net website.
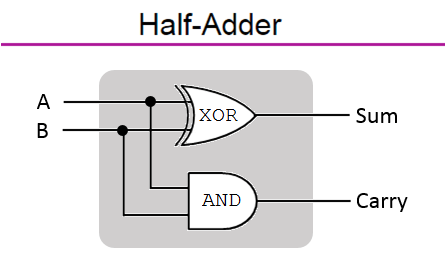
Binary Additions using Logic Gates | 101 Computing

Binary Additions using Logic Gates | 101 Computing
Computers just basically do this but scale up (by quite a lot, in the multiple of billions) with multiple logic gates and process a long string of 0 and 1 and split out the output where we can interpret the outputs to corresponding values. Pretty cool, right? The computer does this task very well and can do many of them simultaneously, hence why we use them. Who would give a job to someone slow and terrible at it? 😜
Now that we understand how computers do operations, how about we try to do their job for once? These will give us some understanding of how to do it? Don’t worry. I won’t ask you to do multiplication or division. We will only do addition and subtraction operations for this lesson, and that would be plenty to take you pretty far in understanding the fundamentals of binary operations. Let get to it, shall we?
Addition
If you look at the picture example above, you will be able to tell how computers do the addition operation. So how do we do it? There are two ways for us to about it. We can either do the same thing as the computers and perform the operations in binary. Or we can convert the binary number into our number, do the calculation, then flip the result back to binary 😜. Personally, I would just do the operations in binary since it is not that complicated; we are talking about adding and subtracting here. How hard can it be, right?
So here is the rule:
- 0+0=0
- 0+1=1
- 1+1=0 and 1 remainder or carry if you prefer to call it that, this number will be use in the next colume
- 0+0+1(carry) = 0
- 0+1+1(carry) = 0 and 1(carry)
- 1+1+1(carry) = 1 and 1(carry)
- If you have carry in the last colume then just write out the carry in the result.
Here is the example:
101011 + 101110 = ???
we can write it like this

If you look up the rules, you will see how we calculate. The order of operation is from right to left. If the number isn’t the same amount of 0 and 1 digits? Simple, just add 0 in front of it 😂 so 11001 = 00011001.
Also, the highest order of magnitude (I will call this order from now) of numbers in binary is the most significant number. Here is an example: 1001 and 11001. 11001 has five digits with the highest order is 1 (remember 0 does not count); therefore, 11001 is bigger. Another example: 10010 and 10000, both have the same order of digits with one at the most significant, now let go down and compare each order in pairs. “10010” is the bigger number if you follow the explanation so far. Order of magnitude is the number of the significant digits minus one since the least significant orders (the far right started at 0). Let look at 10110111; there are eight digits, and the most significant is not 0, so we can say this is the 7th order.
Why does identifying the bigger number matter? Sometimes we have to determine what number is bigger to be able to do some calculation in case the number is negative (I know, I’m not too fond of negative numbers either). I’m sure computers would want to do operations with negative numbers, but sometimes we have to do what we have to do.
Adding negative numbers
Remember I mentioned you could add 0 in front of the numbers to fluff, so they have the same digits? 0 can represent a positive number in binary, and 1 is negative. What do I mean by that? There is a process where we can represent negative binary by adding 1 in front of it and flipping the value(0 to 1 and vice versa). This is what we call 1’s compliment.
Adding a postive and negetive number
If the positive number is bigger than negative number
Let try: 1011001 + (-101011)=??? We did the calculation above, so we know the answer should be 101110 right? So let apply the 1’s complement to get to the answer.
First, we must identify what order of this calculation will be (by looking at the number digits and the sign) 1011001 has seven digits and is positive while 101011 only has six and is negative; therefore, we know the answer will be a positive number. We will then bring all the numbers into the same order. 1011001 is positive; consequently no point in adding 0 in front of it. We can bring 101011 to the sixth order (7 numbers) by adding 1 in front and flipping the value so that it will become 1010100, see what I did there? Now that we have them both in the same order, we can do the regular addition operation. The only difference is that we add the last carry to the least order digit (the furthest to the right)

If the positive number is smaller than the negative number
Using the same example except for this time, we have -1011001 + 101011=??? We are expecting the answer will be a negative number. We are expecting -101110. So how do we going to do this? Here is the checklist:
- First, figure out the highest order, since this highest order is 6th (7 digits) but the number itself is negative we need to make the order into 7th (8 digits).
- Bring all the numbers of the operations to the same order by adding 0 or 1 that corresponding to their sign and taking 1’s compliment. In our case we have 10100110 and 00101011.
- Perform the addition operation
- Taking 1’s compliment of the result, and also dont forget the anwer should be negative

Adding negative numbers
Adding two negative numbers, let try -101011 + (-101110)= ??? You should expect to see the answer to be -1011001. Let find out, shall we?
- Figure the highest order, 6th order for our operations.
- Bring all the number to the same order including the sign, taking the 1’s compliment if negative number and in this case we are doing both. 1010100 and 1010001 .
- Perform the additon operation, adding the final carry (if any) to the lowest orders.
- Taking 1’s compliment of the result. The answer is negative sign.

Subtraction
Now it comes to subtraction. Very similar to how we do addition, as long we follow the rules:
- 0 – 0 = 0
- 1 – 0 = 1
- 0 – 1 = 1 and 1 borrow. Yes just like your student loan you will need to pay it back.
- 1 – 1 = 0
- 0 – 0 – 1(borrow) = 1 and 1 (borrow)
- 1 – 0 – 1(borrow) = 0
- 0 – 1 – 1(borrow) = 0 and 1 (borrow)
Let try the subtraction example, shall we?
What is 1011001 – 101011 = ???
Follow the rules we have:

Do you happen to see the result is a bit familiar by chance? It is the same result as adding 1011001 + (-101011) 🤣. I mean, it should be pretty obvious right? Adding the negative number is the same as subtracting it. Why do I go through all the trouble of converting it to a negative sign using 1’s complement? Well, no particular reason other than giving you additional information. There are many ways to do things, and there is no rigid way, so I’m giving you options. But learning about 1’s complement is a good thing to have as it will take you a long way. I won’t be explaining the same thing for using 1’s complement in subtraction. You can use the example on the addition operations, and instead of following the addition operation rules, just use subtraction rules.
Converting Binary into base 10 number
I know, I know. You went through all of the trouble to understand the binary operation. The result is still a string of 0 and 1, which makes no sense. How would we be able to understand what is its value is? I’m glad you ask. I will show you how to convert them into the base 10 number system (the one we are familiar with)
Base 10 number
What is the base 10 number? As it sounded like, it is a number system where 10 is the base number 🤣What a shocking surprise 😮 . What does it look like, you ask? well 1,2,3,4,5,6,7,8,9,10,11,12… If this looks familiar, you are correct. The number system we are currently using is the base 10 system. So do you know how to calculate the value of it? For example, 4625. What does it make of? Let break it down
4625 = 4000 + 600 + 20 + 5 . Super simple right? So, where is base 10 coming from?
Do you remember what I said about binary orders? The number of digits in a binary number applies the same here. This is 3rd order since there are four digits. Do you know how to represent this number in order of magnitude of base 10? Here is the answer:
4625 = (4 * 103) + (6 * 102) + (2 * 101) + (5 * 100)
Notice how we multiply the number to the base ten raise to the order. If you did not know, 103 is called exponential, and 10 is raised to the 3rd power. So how do you do exponential? 103 = 10 * 10 * 10 = 1000. so 104 = 10 * 10 * 10 * 10 = 10000. Simple as that, the only outlier here is 100 =1. Anything raised to the 0 power is all equal to 1. Now that you understand the order of magnitude and base 10 system. We can easily translate that into a binary system. Let have a look.
Binary number
Do you still remember what binary is? Binary consists of 0 and 1, which is why we called it the base 2 system. Get it? Bi = 2 😉 . You already know how to calculate the value of the base 10 system so just apply the same principle to it except 10 we replace it with 2. super simple right?
Let take a look at 11100111. There are 8 digits in this binary number thus it is 7th order.
11100111= (1 * 27) + (1 * 26) + (1 * 25) + (0 * 24) + (0 * 23) + (1 * 22) + (1 * 21) + (1 * 20)
=(1 * 128) + (1 * 64) + (1 * 32) + (0 * 16) + (0 * 8) + (1 * 4) + (1 * 2) + (1 * 1)
= 128 + 64 + 32 + 4 + 2 + 1 = 231
You have it; you can now convert the binary numbers into numbers where you can understand 😉. Is it a lot of work, eh? You can also just google binary calculator and be done with it, but at least now you understand how to do it and its principle. It is always good to know more before and do things manually before using the tool without understanding how it works, and I hope you learn something from this lecture.
Also, if you want to convert a number back to binary, here is a quick guide:

Conclusion
Congratulation to whoever made it this far! 🥳 you are now more intelligent than you were before reading this… or the same as before (can’t get dumber right?). Now you know how to do binary operations and convert binary to the number. Pretty cool, right? Well then, Professor Laz’s is now done. I shall retire to the shade and take my nap. See you in the next lesson whenever I wake up next time. Have a great week, everyone! Take care!
- Professor Laz

